Sensorsize
Introduction
The sensor size has a decisive influence on the imaging properties of an optical system. In analog times it was generally known that more film area also meant more resolution and sharpness at the same time. The influence of the image angle was also fairly clear. A normal lens for the 35mm format (24mm x 36mm) was 50mm, for the medium format (6cm x 6cm) 80mm and for the large format (let's say 4" x 5") about 150mm. But what influence did this have on the depth of field and why was it possible to use aperture 64 for the large format, but only aperture 22 for the small format?
sensor and pixel size and equivalent focal length
With today's variety of sensors, one immediately loses the overview. This is one of the reasons why camera manufacturers specify the equivalent focal length for their compact cameras. This is the focal length value of a 35mm system that displays an identical image angle as the lens used on the respective sensor. This term is also known for SLR cameras with smaller image sensors than the 35 mm format, so-called 'reduced size sensors'. A widely used sensor is the APS-C sensor, whose edge lengths are 1.6 times shorter than in 35mm format. This factor is called crop factor. Multiply the used focal length with this value and you will get the equivalent focal length in 35mm format. Thus, a 50mm lens on an APS-C sensor corresponds to an 80mm lens (seen purely from the angle of view). The table below shows typical focal length values and their equivalent focal lengths for the crop factor 1.6 (APS-C), 1.33 (e.g. M8 or APS-H) and 2 (4/3rd sensor):
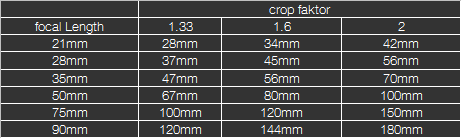
The equivalent focal length is therefore only an aid to evaluate lenses according to the usual criteria in 35 mm format. If we had only used the image angle as a criterion for one lens from the beginning, everything would have been much easier and the lenses for different formats or different sensor sizes could be directly compared. But this has not become common practice, and so one speaks of a 50mm lens instead of a 47° lens for a 35mm sensor. In the table above, the corresponding (diagonal) image angles for the respective focal lengths and equivalent focal lengths are also listed. The image angle is calculated as follows:
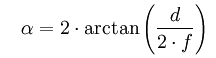
where d represents the format diagonal and f the focal length.
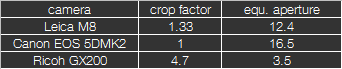
Unfortunately, the sensor size of compact cameras is indicated very cryptically. For example, my Ricoh GX200 has a 1/1.7" sensor. You might think this has something to do with the diagonal of the sensor. Here you are already on the right track, but the value is the diameter of a television tube used in the 50s, and for the sensor to fit in there it must have about 2/3 of its diameter. A 1/1.7" sensor would have a diagonal of (1/1.7*25.4*0.66)mm=9.9mm. In reality the sensor is only 9.2mm, but at least we were close. Much easier is the calculation of the sensor size by using the manufacturer's information regarding the equivalent focal length. With the Ricoh GX200, a 5.1mm lens corresponds to a 24mm focal length in 35mm format, which is a factor of 4.7. So the sensor has an edge length that is 4.7 times smaller than in 35mm format, i.e. 5.1mm x 7.7mm. The table below compares a few cameras with different sensor sizes:

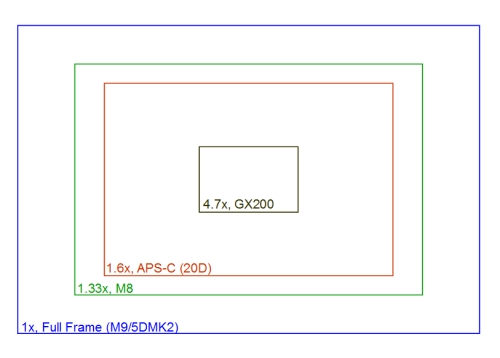
From the table you can read that the chip of the GX200 has only 5% of its surface compared to a 35mm sensor, i.e. an area 20 times smaller! Already an APS-C camera has a surface that is 40% smaller than that of a 35mm sensor, i.e. 2.5 times smaller (see also the graphic above). Nevertheless, the GX200 and the M8 have a comparable resolution, i.e. number of megapixels. This inevitably affects the size of the pixels:
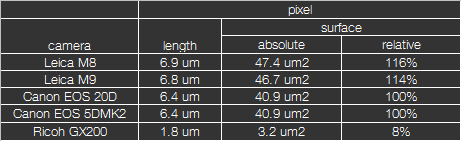
The pixel area was calculated under the assumption that there is no gap between the pixels. This is not completely true, but can be neglected here, the few % are not important. The pixel size of the EOS 5DMK2, a camera with a 35mm sensor, was set to 100%, the pixels of the GX200 have a surface that is 12.5 times (8%) smaller, the pixels of an M8 are slightly larger (1.2 times). That's why compact cameras start to be noisy when the ISO number is slightly higher. If you can use a 5DMK2 without quality loss at ISO400, that's alredy noisy for a compact camera. I don't want to cover it any further, the noise has already been considered sufficiently in other publications.



circle of confusion
When is a picture sharp? There is a concept behind it called circle of confusion. The whole concept is based on the fact that people can see a certain image size at a certain distance. This results in a viewing angle of 50°, which is, for example, the diagonal of an A4 sheet from a distance of 40cm. The human eye has a resolution of approx. 2 angular minutes and since 50° are 3000 angular minutes this is 1/1500 of the diagonal (e.g. the A4 sheet). And exactly this fraction can now be considered as maximum blur on the film, a 1/1500 of the diagonal of the film format. For conventional films this means the following:

Thus, with an 8 "x10" film, the blur circle may be approximately 0.2mm (thus 200um), with a 35mm film only 0.03mm (thus 30um). And because the aperture is blurred by scattering at the aperture lamellas, the circle of distraction gets bigger with increasing aperture. And therefore the maximum adjustable aperture depends on the format. With a 35mm system it is normally an aperture of 16 or 22 (some macro lenses also allow an aperture of 27), but with a large format system it is often an aperture of 64.
And the same applies to digital cameras. As we can see in the table below, the circle of confusion for the Ricoh GX200, for example, is about 3um, i.e. 10 times smaller than for the 35mm format. All these cameras have pixels which are smaller than the circle of confusion, so the pixel size is not the limiting factor.
equivalent aperture
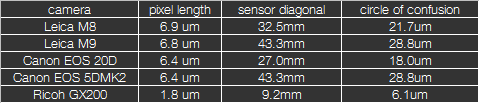
A very important effect of the sensor size is the influence on the aperture or on the ratio aperture / depth of field. If the equivalent focal length is a widely used term, the term equivalent aperture is rarely used. The equivalent aperture is the aperture of a 35mm system where the same depth of field is achieved as with the aperture used for the sensor used in the system. The equivalent aperture is also calculated by simply multiplying the aperture by the crop factor. So if you use a 50mm lens at aperture 4.0 on an APS-C camera, this corresponds to an 80mm lens at aperture 6.4. So you lose (or gain, depending on whether you need more or less depth of field) more than one aperture. One f-stop corresponds to a multiplier of square root of 2, i.e. approx. 1.4, so with a crop factor of 1.4 you would gain/loss exactly one f-stop. For an overview the f-stop row is shown below in half and third f-stops:
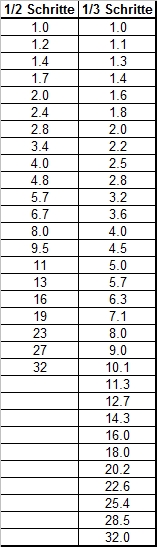
Since stopping down is usually not a problem, the problem of creative depth of field reduction is much more important. This is also the reason why you can take such wonderful pictures with a small depth of field using a large format camera. A 4" x 5" format has a crop factor (related to the diagonal) of 0.27. Aperture 5.6 corresponds to 1.5. With an 8" x 10" format the 'crop' factor is 0.13, aperture 5.6 corresponds to aperture 0.7!

But what about a compact camera? The table below shows the equivalent apertures and focal lengths of the Ricoh GX200:

At 50mm, the largest aperture is 3.5, which corresponds to a aperture of 16.5 in 35mm format, not a big hit! With my M8 I can often only stop down to f-stop 16. That's why it's nice and good when manufacturers indicate 2.8 as the aperture for their compact cameras; unfortunately this doesn't help much with depth of field. But you can use a Ricoh GX200 with 72mm equivalent focal length and a 74 equivalent aperture!
However, the available aperture range remains small with a compact camera. For example, if you can choose between an aperture of 2.0 and 16.0 for a Leica Summicron, i.e. a range of 6 apertures, the Ricoh GX200 has only 4 apertures (e.g. 3.5-12.4 at 10.6mm).
image examples
But let's take a look at all this in picture examples. For this purpose I compared three cameras with different sensors:

The first example shows all cameras with equivalent focal lengths of 50mm, i.e. 35, 50 and 10.6mm (M8, 5DMK2, GX200), all at f-stops 3.5 (or 3.4, the M8 has no third f-stops):



As expected, the 5DMK2 shows the smallest depth of field, followed by the M8. The GX200 already has a nice depth of field at full aperture. However, if we want to achieve the same depth of field with all three lenses, we have to use different apertures:



As the series shows wonderfully that the depth of field areas are now practically the same for all three cameras. The GX200 may even draw a little bit more blurred, which may be due to misalignement of the camera. This is due to the fact that the cameras have a different size and it is therefore difficult to place the sensor center in exactly the same place in the room. But lets not get disturbed by such details. The question remains as to whether the GX200 lens can provide the same imaging performance as a 35 mm lens.
lens test
The following comparison photos should show the quality differences between a compact camera and a camera with an APS-C sensor. Of course this simple test is only exemplary, and one should not forget that a lens for a larger sensor has to let more light through than a lens for a smaller sensor with the same aperture. So although two lenses have the same f-number, the light flow will be much higher with one lens. Thus, the light intensity of a lens can only be compared on the basis of the f-number if one compares lenses that were built for the same sensor, i.e. that illuminate the same image circle.
In order to compare the light intensity of different lenses for different formats, one uses the light value of one lens as a base. This value is calculated from the maximum aperture and the image circle radius, i.e. the area illuminated by the lens. The exact formula is called:
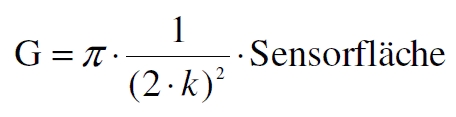
G is the light value, k the maximum aperture value and the image circle is used instead of the sensor area. This results in the following values for the sensor sizes discussed here:

If you now set a lens with aperture 2 on the full-frame sensor to 100%, you get the following table:

Let's first compare lenses on the same sensor: One aperture less means half as much light. As one can deduce
from the formula above, the light value with the same sensor area is thus only dependent on the f-stop number;
we are already used to this comparison of the light intensities of different lenses. But if one compares
different sensors, one sees that a lens throws only 57% of the light onto an APS-C sensor as a lens throws onto
a full-frame sensor with the same aperture value. With the sensor of the GX200 it is only 4.5%.
If you now compare a lens on the GX200 at aperture 3.5 with a lens on a full-frame sensor at aperture 2.0, the
compact lens only has to let through 1.5% of the light compared to the lens on the full-frame sensor. This is
almost the same amount of light as a lens with an aperture of 16 lets through to a full-frame sensor! The Leica
M8 lenses are all fully formatable, which is why I don't use the crop factor 1.3 here to compare the light
value. So we compare lenses that are about 6 f-stops apart in their initial aperture.
But let's have a look at the results. The first two sections are from the GX200 shots at 10.6mm (corresponds to 50mm for full format) and aperture 3.5 and aperture 4.9 (one aperture dimmed) and then two shots with a Leica Summicron 35mm ASPH (also corresponds to approx. 50mm for full format) at apertures 2.0 and 2.8.




If we did not have the background of the discussion with the light value above, we would no longer understand the world! Why can a compact lens deliver virtually the same performance as a highly corrected Leica lens? The 6 f-stops (that's 64 times more light!) difference in the initial aperture explains everything.
Resources
lenses
lens coding
rangefinder camera