Blende
Einleitung
Man sollte eigentlich meinen es gäbe nicht viel über die Blende zu schreiben. Das Thema ist aber viel ergiebiger als man denkt und es gibt einige interessante Details zu berichten. So tauchen immer wieder Fragen auf wie man z.B. den Blendenunterschied zwischen zwei kryptisch angegeben Blendenzahlen berechnet oder wie genau sich eine Blendenreihe zusammensetzt oder gar welchen Einfluss die Anzahl Blendenlamellen auf ein Foto hat. In diesem Artikel werde ich ausserdem auf die Hyperfokaldistanz und die Tiefenschärfe eingehen.
Blendendefinition
Die Blende ermöglicht es, den Lichtfluss durch ein Objektiv zu regulieren. Die Blende ist im Prinzip eine Öffnung mit verstellbarem Durchmesser, durch welches das Licht im Objektiv gelenkt wird. Die maximale Öffnung des Objektivs wird auch die maximale Blende benannt; Blende ist genau genommen eine Abkürzung von Blendenöffnung. Die Blendenzahl ist das Verhältnis zwischen der Brennweite des Objektivs und dem Objektivdurchmesser (Durchmesser der Frontlinse). Je grösser der Durchmesser bei gleich bleibender Brennweite, desto kleiner die Blendenzahl. Die Blendenzahl wird mit dem Buchstaben k abgekürzt, die Brennweite mit f und der Durchmesser der Frontlinse mit d:
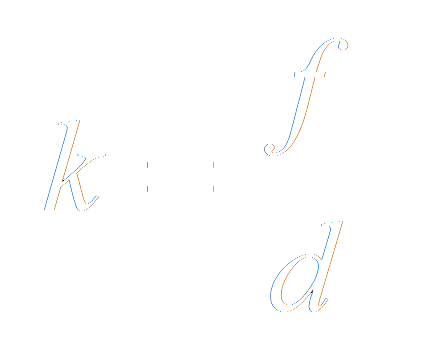
Der Kehrwert dieser Formel wird als Öffnungsverhältnis bezeichnet, also
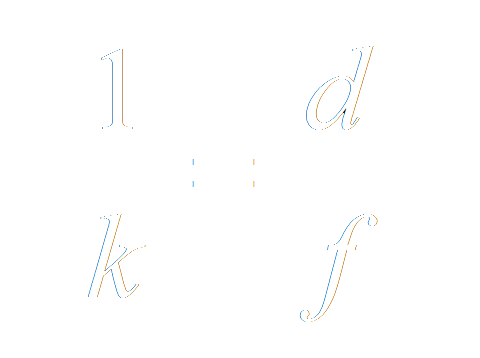
Ein Objektiv mit einer Brennweite von 50mm (beim Kleinbildformat 135 entspricht das in etwa der Formatdiagonalen und daher wird diese Brennweite Normalbrennweite genannt) und einer Öffnung von 25mm hat also eine Blende von f=50mm/25mm=2.0. Wenn man diesen Wert an einem Objektiv nachmisst bemerkt man, dass das Verhältnis meist andere Werte ergibt als die auf dem Objektiv aufgedruckten Angaben. Das liegt daran, dass mit d eigentlich die Eintrittspupille gemeint ist und die entspricht eben nicht genau dem Durchmesser der Frontlinse. So hat mein Summicron mit der Bernnweite von 50mm einen Durchmesser der Frontlinse von 30mm, man würde also für f=50/30=1.66 errechnen, das Objektiv hat aber ‚nur’ eine Blendenöffnung von 2.0. Bei meinem 35mm Objektiv misst der Durchmesser der Frontlinse 25mm, die errechnete Blende ergibt f=35mm/25mm=1.4, auch hier ist die reale Blende des Objektives 2.0. Man kann sich also nicht auf die Formale verlassen, einen ungefähren Anhaltswert gibt sie trotzdem. Nur am Rande; die Blendenzahl ist unabhängig von Lichtverlusten im Objektiv durch z.B. die Absorption und Reflexion in bzw. n den Linsen; diese werden nicht berücksichtigt. Ein Objektiv mit vielen Einzellinsen und derselben Blende wie ein Objektiv mit weniger Einzellinsen lässt dementsprechend unter Umständen weniger Licht durch!


Blendenreihe
Eigentlich gibt es unendlich viele Blendenwerte, zur Übersichtlichkeit hat man sich aber auf ein paar fix definierte Werte festgelegt und Objektive werden meist so konstruiert, damit sie mit einem dieser Blendenschritte übereinstimmen. Wenn man einen Numerator n zur Hilfe nimmt, wobei n einer aufsteigende Zahlenfolge entspricht, kann man mit der folgenden Formel ganz einfach ganze Blendenschritte berechnen, wenn n ganzzahlig ist und eine beliebige andere Folge, wenn man n entsprechend dimensioniert, z.B. 0.5er Schritte für Halbblenden:
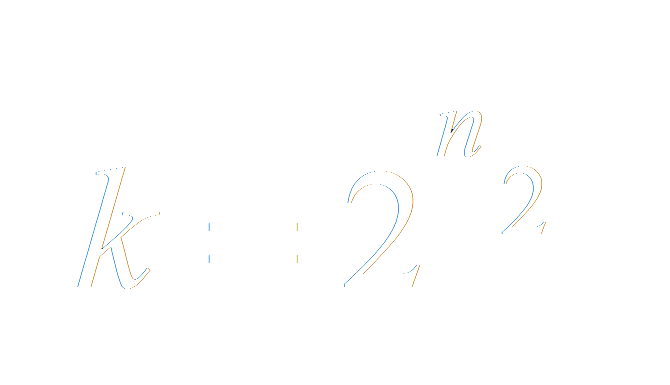
Daraus ergeben sich folgende Blendenreihen für volle, halbe und drittel Blendenschritte:
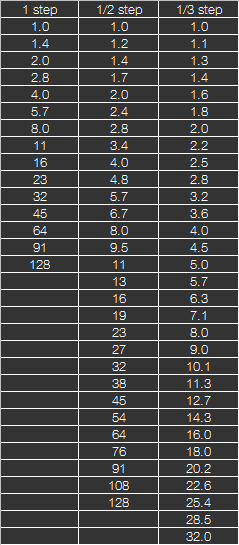
Bei einem vollen Schritt verdoppelt sich die Öffnung der Blende und damit kann doppelt so viel Licht durch die Blende hindurch dringen. Der Radius wird aber nur um den Faktor Wurzel(2)=1.4 grösser, da sich die Fläche im Quadrat des Radius verhält. Die Blendenzahl wird deshalb auch nur um den Faktor 1.4 grösser. Jede zweite Blende verdoppelt sich aber. Man muss sich also nicht die ganze Blendenreihe merken, es reicht, wenn man sich 1.0 und 1.4 als Anfangswerte merkt, alle anderen Werte errechnet man sich durch Verdoppelung. Die übernächsten Werte werden wieder durch Verdoppelung errechnet. Das wurde offensichtlich bei der ursprünglichen Definition der Blendenreihe auch so gemacht, man sucht nämlich den Wert 5.7 und 23 vergeblich auf seinem Objektiv.
Wird man bei vollen Blendenstufen den nächsten Wert einfach durch multiplizieren des vorhergehenden Wertes mit Wurzel(2) bzw. 2^(1/2) multiplizieren, muss man bei halben Blendenstufen einfach den Multiplikator 2^(1/4)=1.19 bzw. bei 1/3 Blendenstufen den Multiplikator 2^(1/6)=1.12 verwenden.
Die Hersteller sind sich natürlich nicht ganz einig, ob man nun 1/3 Schritte oder ½ Schritte einführen soll. Bei elektronischen Blenden kann man das heute zumeist selbst definieren, ob man nun lieber ½ oder 1/3 Schritte möchte. Bei Objektiven mit einem Blendenring der mechanisch aufgebaut ist hat man natürlich diese Flexibilität nicht. Bei Leica werden z.B. ½ Schritte verwendet, bei Objektiven von Zeiss für das Leica M System aber 1/3 Schritte. Ich selber bevorzuge ½ Schritte weil das für mich genau genug ist und ich mir nicht so viele Zahlen merken muss. Ausserdem kann ich am Zeitenrad (das verwendet praktisch immer 0.5er Schritte) zweimal klicken und auch am Blendenring zweimal und schon habe ich wieder die gleiche Belichtung eingestellt. Auch die Empfindlichkeitswerte (ISO)habe ich deshalb auf 0.5er Stufen festgelegt. Aber da wird wohl jeder seine eigene Vorlieben haben.

Manche Hersteller scheinen sich um Blendenreihen gar nicht zu kümmern. So werden an meiner Ricoh GX200 nicht nur 1/3 Schritte verwendet, sondern auch noch andere absolute Blendenwerte je nachdem welche Brennweite eingestellt ist. Das ist natürlich absolut verwirrend und man kann mit all den Werten überhaupt nichts anfangen. Offensichtlich wurde bei jeder Zoomstufe einfach die maximale Blendenöffnung errechnet und von dort aus eine Blendenreihe ermittelt. Die untenstehende Tabelle zeigt diese Werte.
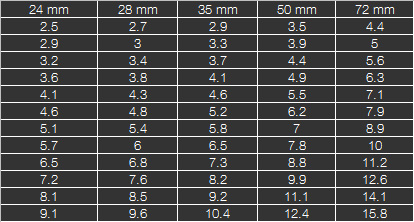
Aber wie errechnet man nun den Blendenunterschied z.B. zwischen (bei 28mm) 4.3 und 5.4?
Differenz zwischen zwei Blendenstufen
Die Blendenschritte berechnen sich wie schon gesagt mit der folgenden Formel:
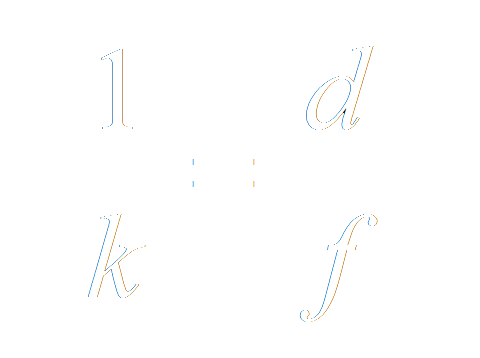
Wir lösen diese nun nach n auf und erhalten:
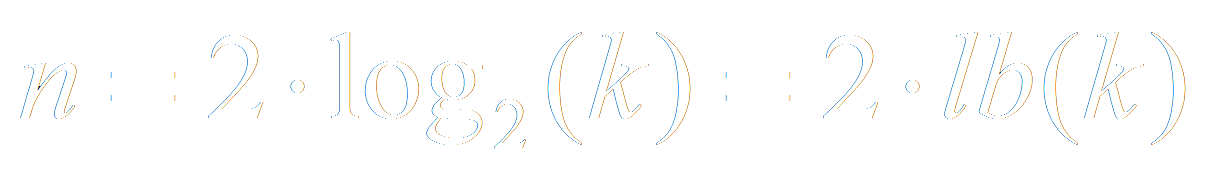
Wobei lb der binäre Logarithmus, also der Logarithmus mit der Basis zwei ist.
Und da wir uns für die Differenz zwischen zwei Werten n1 und n2 interessieren müssen wir nur noch die Differenz bilden:
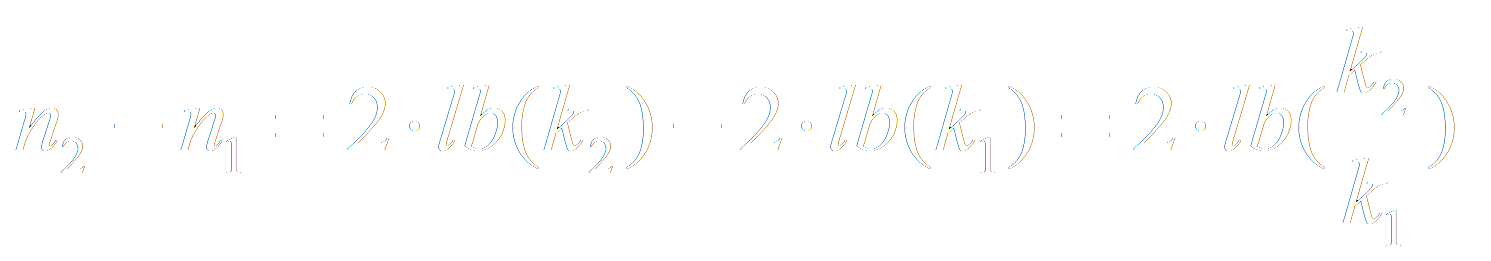
Das obige Beispiel mit k1=4.3 und k2=5.4 ergibt demnach einen Unterschied von 0.66, also 2/3 Blendenstufen. Falls Sie übrigens keinen lb auf ihrem Taschenrechner finden nehmen sie einfach den 10er Logarithmus (log) und dividieren durch log(2).
Zum Glück muss man diese Rechnerei nicht immer veranstalten, wenn man im Feld ist. Dank der standardisierten Blendenreihe geht das viel einfacher (wenn man sich einmal die Werte gemerkt hat).
Tiefenschärfe und Hyperfokaldistanz
Beim Abblenden erhöht sich die Tiefenschärfe. Doch wie definiert sich die Tiefenschärfe.
Eigentlich ist nur genau der Punkt scharf, auf den man den Fokus gelegt hat bzw. die Ebene parallel zur
Film oder Sensorebene, die durch diesen Punkt geht (ich lasse jetzt einmal Scheinpflug und co. ausser
Acht). Da aber das Auge eine gewisse Unschärfe erlaubt, um einen Gegenstand noch als scharf zu sehen,
werden auch Punkte vor bzw. hinter der Eben noch als scharf angesehen. Diese Punkte werden als kleine
Unschärfekreise abgebildet. Doch wie gross darf ein solcher Unschärfekreis denn überhaupt
sein. Da das menschliche Auge eine ungefähre Winkelauflösung von 2 Winkelminuten hat und das
Gesichtsfeld 50 Winkelgrad beträgt entsprechend diese 2 Winkelminuten etwa dem 1500stel des
Gesichtsfeldes. Nimmt man nun an, dass man ein Foto gerade so hinlegt, dass die Diagonale das Gesichtsfeld
ausfüllt muss man auf der Diagonalen eine Auflösung von 1500 Punkten erzeugen. Und da man das
Foto von einem Sensorabbild oder einem Film vergrössert hat, muss dieser dieselbe Auflösung
besitzen (wir nehmen mal an, dass während des Vergrösserungsprozesses
nichts
verloren geht). Das Kriterium ist also 1500stel der Sensor- oder Filmdiagonalen. Dies ergibt die bekannten
30um Zerstreuungskreisgrösse (COC=Circle of Confusion) für den Kleinbildfim 135 bzw. den
Vollformatsensor.
Da dieser Unschärfekreis sich auf die Formatdiagonal bezieht, wird er mit abnehmender Formatdiagonale auch kleiner, z.B. bei einem APS-C Sensor mit einem Crop Factor von 1.6 um den Faktor 1.6 kleiner, also statt 30um (genau sind es 29um) nur noch 18um.
Interessant ist nun die Distanz, bei der sich die Tiefenschärfe bis ins unendliche erstreckt. Stellt man diesen Wert ein, ist alles von der Hälfte der eingestellten Distanz bis unendlich scharf. Die sogenannte Hyperfokaldistanz errechnet sich wie folgt:
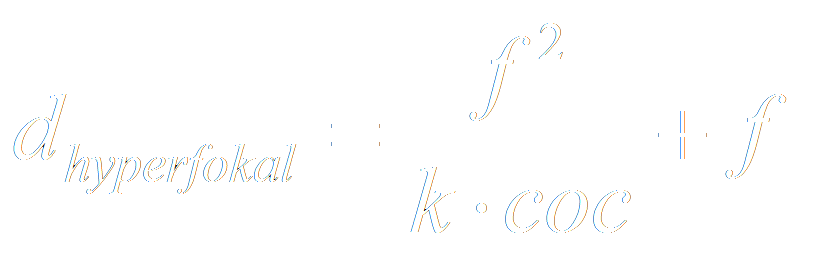
Wobei f dem Brennweite, k dem Blendenzahl und coc dem Circle of Confusion, also dem Unschärfekreis bzw. Zerstreuungskreis enstpricht. Setzt man z.B. f=50mm, k=8 und den coc auf 30um erhält man eine Distanz von 10.4m. Stellt man diese Distanz am Objektiv ein, ist alles von 5.2m bis unendlich scharf.
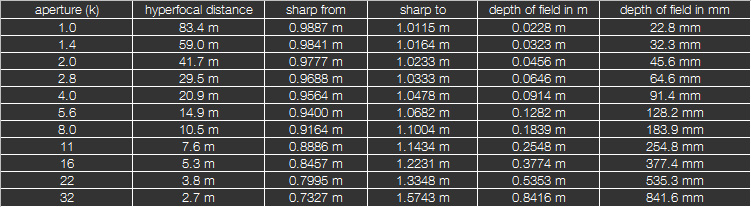
Die untenstehende Tabelle stellt sowohl die Tiefenschärfe wie auch die absoluten Tiefenschärfegrenzen für das Kleinbildformat und ein 50mm Objektiv dar, wenn der Fokus auf 1m engestellet wurde:
Ist man in der glücklichen Lage und das verwendete Objektiv besitzt noch Markierungen für die Tiefenschärfe, kann man natürlich ganz einfach einen beliebigen Tiefenschärfebereich einstellen oder ganz einfach die Hyperfokaldistanz finden indem man das unendlich Zeichen auf die Markierung für die Tiefenschärfe bei der jeweiligen Blende stellt.

Man muss jedoch beachten, für welchen Sensor die Markierungen für die Tiefenschärfe am Objektiv berechnet wurden. Da man Vollformat-Objektive auch an Kameras mit einem APS-C oder APS-H Sensor montieren kann, muss man berücksichtigen, dass die Tiefenschärfeskala für das Vollformat berechnet wurde. Bei einem APS-H Sensor muss man deswegen knapp eine Blende mehr abblenden, bei einem APS-C Sensor sind es knapp zwei Blenden, damit die Skala dem korrekten Tiefenschärfebereich enstpricht. Dies wird in der untenstehenden Tabelle veranschaulicht:
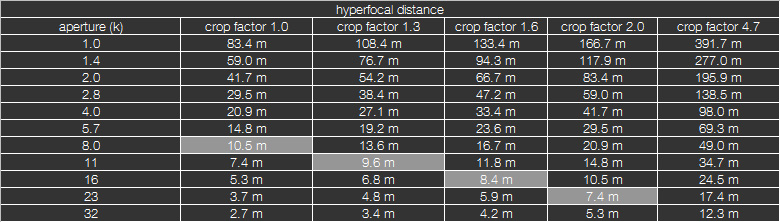
Ich möchte noch darauf hinweisen, dass ein 50mm Objektiv an einem kleineren Sensor einen kleineren Bildwinkel abbildet. Darum ist ein 50mm an einem APS-C Sensor bezüglich des Bildwinkels äquivalent einem 80mm Objektiv an einem Kleinbildsensor. Dies wird ausführlicher im Artikel Sensor beschrieben.
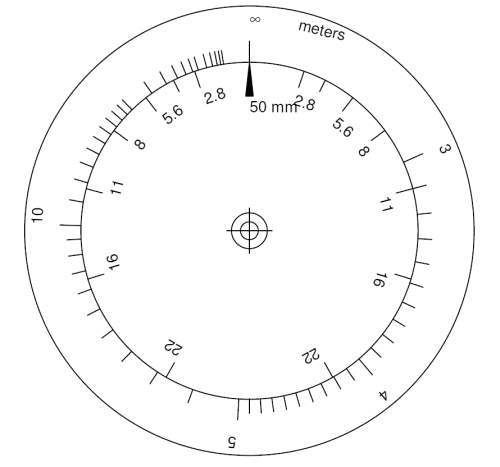
Wenn man diese Markierungen bei einem Objektiv vermisst kann man sich am einfachsten ein entsprechendes Einstellrad selber herstellen. Es gibt die Software dofmaster, die das Erstellen eines solchen Tiefenschärferechners auf einfachste Art erlaubt.
Ein Beispiel für einen solchen Tiefenschärferechner ist unten abgebildet:
Einfluss auf die Abbildungsleistung
Die Blende hat einen ganz wesentlichen Einfluss auf die Abbildungsleistung eines Objektives. Je besser ein Objektiv korrigiert ist, desto weniger wird man diesen Effekt wahrnehmen und desto brauchbarer ist ein Objektiv schon bei voll geöffneter Blende. Praktisch alle Abbildungsfehler werden durch ein leichtes Abblenden vermindert. Das wird schon aus den Datenblättern der Hersteller ersichtlich, die z.B. bei der MTF (der Modular Transfer Funktion) eine bessere Kontrastwiedergabe des Objektives auszeichnen. Unten ist die MTF für das Leica Summicron 35mm ASPH abgebildet. Deutlich ist der Zuwachs an Kontrastleistung bei Blende 5.6 relativ zu Blende 2.0 ersichtlich. Die Kurvenpaare entsprechen 5, 10, 20 und 40 Linienpaare pro mm (lp/mm), die gestrichelte Kurve steht für sagittale Strukturen, die durchgezogene Kurve für tangentiale Strukturen; copyright Leica.
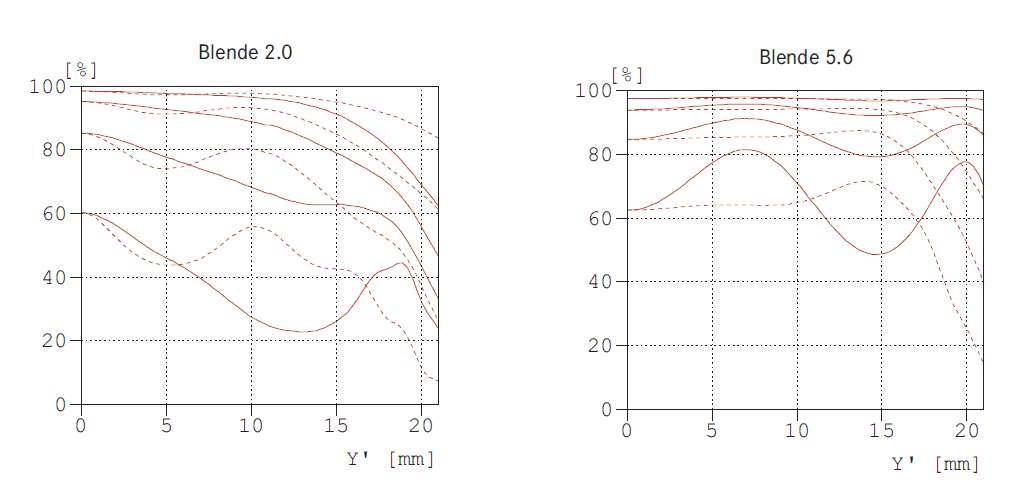
Die MTF sagt auch aust, dass ein Objektiv am Rand meist weniger scharf abbildet als im Zentrum. Beispiele dazu findet man im Artikel Objektiv.
Als Beispiel für eine Minderung von Abbildungsfehlern möchte ich hier die Vignettierung zeigen, die beim abblenden deutlich zurückgeht. Die Aufnahme wurde mit einem Canon EF24-105mmf4.0L-ISM bei Blende 4.0 und Blende 8.0 erstellt, die zweite Aufnhame ist also um zwei Blenden abgeblendet.


Ein weniger bekannter Effekt ist, dass durch zu starkes Abblenden die Schärfeleistung wieder abnimmt, da es zu Streueffekten an den Blendenlamellen kommt. Das hat auch zur Folge, dass man bei kleineren Sensorformaten weniger stark abblenden kann als bei grösseren Sensoren, ganz einfach weil bei grösseren Formaten der noch tolerierbare Unschärfekreis grösser ist, wie das im Text oben erklärt wurde. Darauf wurde auch im Artikel Sensorgrösse eingegangen. Ich möchte hier nur den Effekt bei einem Objektiv aufzeigen und zwar bei einem sehr gut korrigierten Leica Simmicron 35mmf2.0 ASPH, also einem Objektiv mit asphärischer Korrektur. Die Ausschnitte wurden jeweils aus der Nähe des Bildrandes ausgeschnitten. Die Bildreihe umfasst Aufnahmen bei Blende 2.0, 4.0, 8.0 und 16.0, also Aufnahmen im Abstand von jeweils zwei Blendenstufen. Von Blende 2.0 auf Blende 4.0 ist ein deutlicher Zuwachs an Kontrast und Schärfe sichtbar, man beachte z.B. die Äste im Vordergrund oder den Rasen im Hintergrund. Das hat übrigens nichts mit der Tiefenschärfe zu tun (zumindest beim Rasen), bei einem 35mm Objektiv und Blende 2.0 ist die Hyperfokaldistanz bei ca. 20m, es sollte also alles von 10m bis unendlich scharf sein (bei 30um Unschärfekreis). Die Äste im Vordergrund sind. ca. 25..30m entfernt, der Pool ca. 50m.
Bei Blende 8.0 ist der Zenit schon überschritten und bei Blende 16.0 ist nochmals eine leichte Verschlechterung der Bildqualität ersichtlich. Bei Blende 16.0 ist schon fast wieder die Bildqualität von Blende 2.0 erreicht. Das ist sehr wahrscheinlich der Grund, warum man das Objektiv nicht weiter abblenden kann.




Blendenlamellen
Die Form und Anzahl der Blendenlamellen hat einen ausschlaggebenden Einfluss auf die Abbildung der unscharfen Bereiche eines Bildes. Die Art und Weise wie unscharfen Bereiche abgebildet werden wird auch das Bokeh (von jap. boke „unscharf“ oder „verschwommen“) eines Objektivs genannt. Das kommt ganz einfach daher, dass eine Blende mit weniger Lamellen eine weniger runde Öffnung bildet verglichen mit einer Blende mit vielen Lamellen. Die unscharfen Bereiche werden aber genau diese Form wiedergeben und sobald diese Bereiche nicht mehr als runde Flächen abgebildet werden erscheinen sie dem Auge weniger harmonisch. Wir werden das weiter unten noch genauer betrachten.

Als erstes schauen wir uns zum Vergleich zwei verschiedene 50mm Objektive an, ein Canon und ein Leica Normalobjektiv (s. Abbildung oben). Das unten dargestellte Objektiv ist ein Leica Summicron bei Blende 2.0, 8.0 und 16.0. Sehr schön sieht man, wie die Öffnung relativ rund durch die Blendenlamellen gebildet wird. Das Objektiv besitzt 8 Blendenlamellen.



Das Canon Objektiv besitzt aber nur 5 Lamellen. Wie man auf den Bildern unten sieht, wird durch eine kleine Anzahl Blendenlamellen eine weniger runde Öffnung gebildet. Die drei Bilder zeigen das Objektiv bei Blende 1.8, 8.0 und 22.0; das Canon Objektiv kann man also eine Blende stärker abblenden als das Leica Objektiv.



Der Einfluss auf die Bildwiedergabe wird in den nächsten Abbildungen gezeigt: