No Startrails
Enleitung
Aufnahmen des nächtlichen Himmels beeindrucken immer wieder aufs Neue. Möchte man auf der Aufnahme Sternbilder erkennen müssen diese scharf abgebildet werden. Die Sternbewegung (bzw. die Erdrotation) muss durch eine kurze Belichtungszeit eingefroren werden. Es wird hier davon ausgegangen, dass man keine aktive Nachführung verwendet, die Kamera ist also fix auf einem Stativ montiert. Bei einer Nachführung wird die Kamera entgegengesetzt zur Erddrehung bewegt. Ein Stern im Bild bleibt bei gut ausgerichteter Montierung immer an derselben Stelle auf dem Film/Sensor und kann lange (mehrere Minuten) belichtet werden. Eine solche Nachführung ist aber nicht ganz trivial und auch kostspielig und soll hier nicht weiter betrachtet werden.
Berechnungen
Die maximal mögliche Belichtungszeit hängt von verschiedenen Faktoren ab:
- Brennweite des Objektivs und damit vom Öffnungswinkel des Objektivs
- Fläche des verwendeten Films bzw. Sensors (was wiederum einen Einfluss auf den Öffnungswinkel hat)
- Maximaler Unschärfekreis auf dem Sensor bzw. Film der eine noch scharfe Wiedergabe ermöglicht


Aus diesen Werten berechnet man die maximale Belichtungszeit, bei der die Sterne gerade noch scharf auf dem Sensor/Film abgebildet werden. Die Erde rotiert an einem Tag um ihre eigene Achse, also 360° in 24h bzw. 15° pro Stunde, 0.25° pro Minute oder 0.004° pro Sekunde usw. Diese relative Sternbewegung rechnet man auf die vom Objektiv auf den Film bzw. den Sensor projizierte Abbildung um.
Aus den Daten für das verwendete Kamera – Objektivsystem lässt sich der Öffnungswinkel berechnen. Der Öffnungswinkel wird relativ zur Bilddiagonalen angegeben, entspricht also der Formatdiagonalen. Der Unschärfekreis ist ein Bruchteil dieser Formatdiagonalen und derselbe Bruchteil kann auch auf den Öffnungswinkel angewendet werden (das gilt zumindest für die Bildmitte). Dem Unschärfekreis entspricht also ein maximaler Winkel, bei dem eine noch scharfe Abbildung eines Sternes möglich ist. Nun errechnet man die Zeit in welcher ein Stern sich durch diesen Winkelbereich bewegt und schon hat man die maximale Belichtungszeit, um Sterne noch scharf abzubilden. Die Berechnung muss für jedes verwendete Objektiv bzw. für jede Brennweite durchgeführt werden.
Zur Berechnung: Die Format Breite ist b, die Diagonale d und die Brennweite f und der halbe Öffnungswinkel in der Horizontalen α. Dann ergibt sich aus
Mit einem Unschärfekreis von z.B. b/1200 ergibt sich dann ein maximaler Bewegungswinkel αmax durch:
Die Rotationsgeschwindigkeit in der Erde ist 360°/Tag, i.e. 0.004°/sec und daraus ergibt sich die
maximale Belichtungszeit in der der Unschärfekreis durchfahren
wird. Mit
findet man durch einfaches umformen und einsetzen
Beim Fish-Eye Objektiv kann man einfacher vorgehen. Der diagonale Öffnungswinkel ist hier (bei einem 180° Fish Eye das formatfüllend abbildet) ganz einfach 180°. Damit findet man bei einem Unschärfekreis von z.B. d/1440 (das entspricht in etwa dem oben genannten Unschärfekreis von b/1200 bei einem Setenverhältnis von 2:3)






Für Sensoren wird die Pixelbreite bzw. Pixeldiagonale als Unschärfekreis gesetzt, welche man aus der Sensorfläche und der Anzahl Pixel errechnet. Es wird vereinfacht angenommen, dass zwischen den einzelnen Pixeln keine Anstände vorhanden sind.
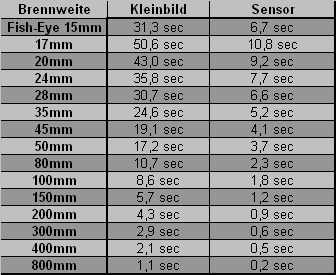
Die untenstehende Tabelle gilt:
- für Kleinbildfilm (24mm x 36mm, obere Tabelle),
- für einen 8MP Sensor im APS-C Format (15mm x 22.5mm, 2336 x 3504 Pixel, 8.2MegaPixel, Verlängerungsfaktor 1.6, z.B. Canon EOS20D) und
- für einen Vollformatsensor mit 21MP (5616 x 3744 Pixel, z.B. Canon EOS5DMark2)
Da bei den beiden Digitalkameras die Pixelgrösse praktisch identisch sind wird in der Tabelle nur ein Wert für beide Kameras/Sensoren berechnet.
In der Praxis
Praxistests zeigen, dass mit dem erwähnten APS-C Sensor und einem Fish-Eye Objektiv noch scharfe Aufnahmen bis 20 Sekunden gemacht werden können, die TAbelle ist hier also eher konservativ.
Wie aus den Tabellen ersichtlich, sind vor allem mit Weitwinkelobjektiven passable Belichtungszeiten erreichbar. Ausserdem ist es ausschlaggebend, wie gross die maximale Blendenöffnung eines Objektivs ist. Das von mir verwendete Fish-Eye hat eine Öffnung von 1:2.8. Für Himmelsaufnahmen arbeite ich oft bei 400 bis 800 ASA. Besonders bei 400ASA sind die meisten APS-C Sensoren noch relativ rauscharm und man erreicht gute Bildergebnisse. Ansonsten kann man auch Rauschreduktionsprogramme wie z.B. Neatimage verwenden.
Es empfiehlt sich aber auf jeden Fall, für jedes Bild ein Dunkelbild (Dark Frame) zu erzeugen und vom eigentlichen Bild abzuziehen. Gücklicherweise muss man dafür nicht gleich zum Astrofreak mutieren und ein externes Programm zur Hilfe nehmen (zum Beispiel Iris). Die meisten digitalen Spiegelreflex-Kameras ermöglichen eine automatische Dark Frame Reduktion. Man braucht diese Automatik nur zu aktivieren. Die Aufnahmezeit verdoppelt sich dabei allerdings, da die Kamera für jede Aufnahme ein Dark Frame erzeugt und dieses automatisch vom gerade aufgezeichneten Bild abzieht. Eine Ausdnahme ist hier die Canon EOS 5DMark2, bei der Darkframes nach max. 5 Aufnhamen abgezogen werden können. Man kann also 5 Aufnahmen ohne unterbruch machen. Zusätzlich kann man es der Kamera überlassen zu entscheiden, ob ein Darkframe überhaupt nötig ist; dadurch kann man noch mehr Aufnahmen ohne Wartezeiten durchführen. Macht man den Abzug extern, reicht natürlich ein Dark Frame für eine Serie von Aufnahmen unter ähnlichen Umgebungsbedingungen (Temperatur!) und gleicher Belichtungszeit und Empfindlichkeitseinstellung.


Belichtet man trotz den Vorgaben ein wenig länger, kann man unter Umständen auch noch akzeptable Resultate erhalten. Die Sterne auf dem Sensor/Film werden zwar nicht mehr absolut scharf bzw. punktförmig abgebildet, doch für kleinere Vergrösserungsformate ist ein grösserer Unschärfekreis akzeptabel. Das Bild unten wurde 60 Sekunden mit einem Fish-Eye Objektiv bei der maximalen Öffnung von 2.8 belichtet. Durch die längere Belichtungszeit werden leuchtschwächere Sterne abgebildet. Für die Abschätzung der maximalen Belichtungszeit hilft folgende Abschätzung: Man errechnet für einen bestimmten Sensor die maximale Vergrösserung, die noch scharfe Abzüge bzw. Ausdrucke erlaubt. Vergrössert man nun das Endresultat nur ein viertel so gross (also jeweils halbe Seitenlänge) so darf bei der Aufnahme doppelt so lange belichten werden.

Zusatz Mai 2008, erweitert April 2010
Bei der Übersetzung des Textes ins Englische ist mir aufgefallen, dass die Sternbewegung in diesem
Artikel ungenau diskutiert wurde. Der Sternenhimmel bewegt sich relativ zur Erde, da sich die Erde wie oben
erwähnt einmal in 24Stunden um ihre Achse dreht. Der Himmelsäquator dreht sich dabei mit der
höchsten Geschwindigkeit, nämlich genau mit den 360Grad in 24h. Schaut man aber zum Himmelspol,
drehen sich dort die Sterne um sich selbst
. Da wir bei der Aufnahme keine Details des Sterns
wiedergeben (der Stern wird ja nur als weisser Punkt bzw. als weisse Fläche wiedergegeben) kann man einen
Stern der genau im Pol steht beliebig lange aufnehmen, es bleibt immer eine weisse Kreisfläche/Punkt
(natürlich wird es irgendwann einmal Tag…). Die Bewegung nimmt also zu den Polen hin ab. Da man nun
aber mit einem Weitwinkelobjektiv immer eine Region des Himmels aufnimmt, die Sterne aller möglichen
Winkel zwischen Pol und Äquator beinhaltet wird die Belichtungszeit so ausgelgt, dass der Stern mit der
maximalen relativen Geschwindigkeit noch scharf abgebildet wird. Es wäre aber sehr kompliziert bei jeder
Belichtung abzuschätzen wie weit die Sterne vom Himmelspol bzw. vom Himmelsäquator entfernt sind,
die sich auf der Aufnahme befinden. Ich habe deswegen gänzlich darauf verzichtet und für meine
Berechnungen immer die maximale Sternbewegung betrachtet. Bei Aufnahmen von Regionen um den Pol hat man
dadurch einen zu konservativen Wert, dafür ist die Formel/Tabelle einfach.
Um die Sache weiter zu vereinfachen ist es vorteilhaft sich auf ein Objektiv mit einer Belichtungszeit zu konzentrieren. Ich verwende fast ausschliesslich mein Fish Eye Objektiv für Himmelaufnahmen und experimentiere mit verschiedenen ISO Einstellungen. Dadurch lernt man die Wiedergabe auf dem Sensor genauer kennen und kann einschätzen welche Folgen es hat wenn man einmal länger als berechnet belichtet
Ich möchte auch noch einen Zusatz zum Dunkelbildabzug machen. Wie oben besprochen gibt es zwei Wege zum Bild mit Dunkelbildabzug. Der kamerainterne Weg ist der einfachere. Man kann die Sache praktisch vor Ort erledigen und muss sich später nicht mehr darum kümmern. Ausserdem sind die Resultate sehr akkurat, da für jedes Bild ein exakt passendes Dunkelbild generiert und im RAW Format abgezogen wird. Es wird also keine Konvertierung vorgenommen. Wird der Dunkelbildabzug extern erledigt, wird das Bild immer erst eine Beyer Konvertierung unterzogen. Die Pixel eines Sensors könne ja nicht direkt Farben unterschieden. Deswegen werden die Sensoren mit Farbfiltern versehen. Es ist nun aber nicht der Fall, dass ein 8MP Sensor 8 Millionen Sensoren für jede der drei Grundfarben Rot Grün Blau (RGB) besitzt sondern nur insgesamt 8 Millionen Pixel (eine Ausnahme bildet der Feavon Sensor). Bei konventionellen Sensoren werden die hälfte der Pixel mit einem Grünfilter, ein Viertel mit einem Blaufilter und das letzte Viertel mit einem Rotfilter versehen. Es werden mehr Grünfilter verteilt um die Augensensitivität, die im grünen Licht maximal ist, nachzuahmen. Die Farbinformation hat also nicht etwa eine Auflösung von 8MP sondern wird aus 4MP grün und je 2MP Rot und Blau zusammengerechnet. Das Rauschen wird dabei entsprechend verrechnet, da ein jpg oder tif Bild ja 8Megapixel mit RGB Werten besitzt. Die Farbinformation wird durch Einbezug der Nachbarpixel durchgeführt. Ebenso wird das Rauschen eines jeden Pixels in diese Rechnung mit einbezogen. Das Rauschen ist im jpg oder tif file also nicht mehr das originale Pixelrauschen sonder ein entsprechend verrechneter Wert aus mehreren Pixeln. Es ist viel genauer den Rauschabzug direkt mit den unkonvertierten Daten auszuführen. Deswegen ist der kamerainterne Dunkelbildabzug nicht nur ein sehr bequemer weg sondern auch ein sehr akkurater Weg. Ausserdem ist das Endresultat ein RAW Bild das optimal weiterverarbeitet werden kann und nicht ein konvertiertes tiff oder jpg Bild. Ein weiteres Plus ist, dass man nicht mit einer Menge von Originalaufnahmen, Dunkelbildern und bearbeiteten Originalbildern hantieren muss (evtl. auch noch mit gemittelten Dunkelbildern und deren Einzelaufnahmen), sondern nur mit einem einzigen RAW file
Der Nachteil des Kamerainternen Dunkelbildabzuges ist aber, dass man nach jeder Aufnahme warten muss bis die Kamera den Dunkelbildabzug vorgenommen hat. Am einfachsten man probiert den internen Dunkelbildabzug aus und wenn einem die Warterei nicht allzu sehr stört wird man dabei bleiben. Vielleicht wird es irgendwann einmal eine Kamera geben die es erlaubt ein Dunkelbild für eine Anzahl folgender Aufnahmen zu verwenden und dann nach einer Serie den Abzug schnell erledigt. Ansatzweise ist das ja schon bei der Canon 5DMark2 integriert, allerdings kan man den Zeitpunkt des Dunkelbildabzuges nicht selber festlegen. Eine alternaive Möglichkeit wäre, dass der RAW Konverter erlaubt ein Dunkelbildabzug vorzunehmen. Aber im Moment gibt es meines Wissens keine Software, die einen RAW Dunkelbildabzug erlaubt. Falls Sie mehr wissen, würde ich mich über ein E-Mail freuen.
Zusatz 6.3.2011
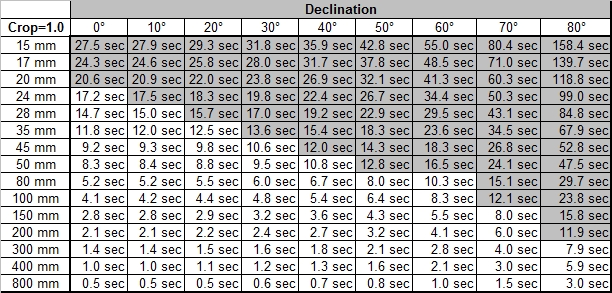
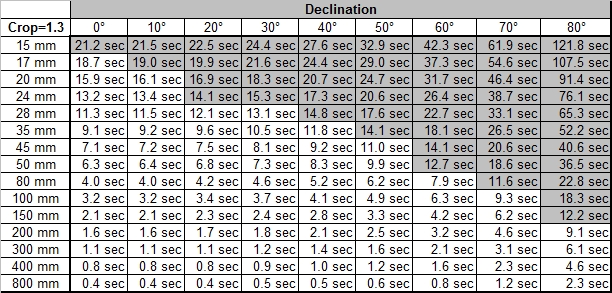
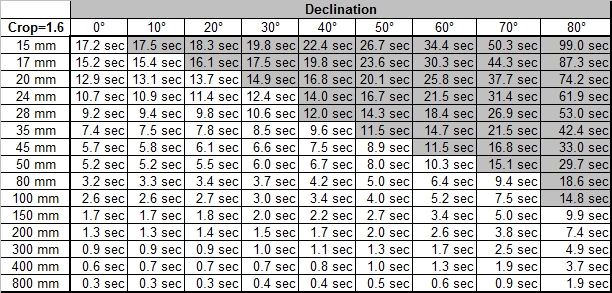
Wie oben erwähnt gilt die maximale berechnete Belichtungszeit für Sterne am Himmelsäquator. Sind die Sterne einen gewissen Winkel vom Himmeläquator Richtung Himmelspol entfernt (das ist dann die Deklination) wird ihre relative Bewegung zur Erde immer geringer. Daher kann man diese Sterne länger Belichten. Da aber ein Objektiv immer einen bestimmten Himmelsbereich abdeckt, muss man nun die Belichtung wählen, die dem Sten mit der kleinsten Deklination entspricht. Und weil gewisse Objektive schon mehr als 90° Öffnungswinkel messen, muss man bei diesen Objektiven ganz besonders vorsichtig sein, dass man nicht eine allzu lange Belichtung wählt und die Sterne am Rand des Bildes unscharf abgebildet werden. Ich habe deshalb in der Tabelle die Felder grau hinterlegt, bei welchen das Objektiv einen Winkel aufweist, der von Pol gemessen der maximalen Deklination eines Sternes in der jeweiligen Kolonne entspricht. Ein Beispiel soll dies verdeutlichen. Hat ein Objektiv eine diagonale Öffnung von 65°, so werden alle Felder für Deklinationen über 90°-65°=25° grau markiert. Wenn man den Pol aber mittig ins Bild setzt, kann man natürlich entsprechend länger belichten, es kommt ja nur auf die Sterne mit der kleinsten Deklination im Bild an.
Es wurde auch angesprochen, dass die Annahme des Pixelabstandes als Unschärfekreis zu konservativ ist.
Verschiedene Praxistest haben ergeben, dass man besser den Crop Faktor einberechnet. Das entspricht der
Annahme, dass eine Aufnahme später ausgedruckt wird und man diese unter einem bestimmten
Betrachtungswinkel anschaut. Da der Winkel immer ungefähr gleich ist, also grössere Bilder auch aus
grösserer Distanz betrachtet werden, ist die Auflösung der Kamera in einem ersten schritt nicht
relevant, wenn sie eine gewisse Schwelle überschritten hat. Diese Schwell liegt bei ca. 3MPixel für
A4 und stellt heute keine wirkliche Grenze mehr dar. Genau diese Betrachtung führte übrigens auch zu
dem Unschärfekreis von 0.03mm für Kleinbildfilm. Bei einem Crop Faktor ist der Unschärfekreis
dementsprechend einfach 1.3 mal kleiner, weil die Aufnahme später 1.3mal mehr vergrössert werden
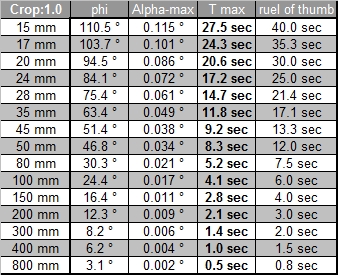
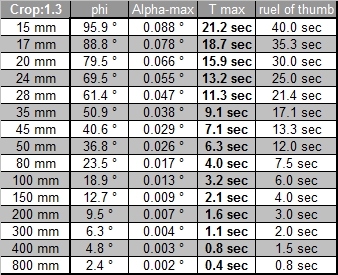
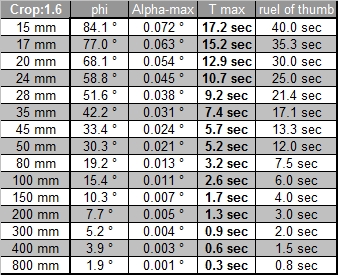
muss (relativ zum Kleinbildfilm) um auf die gleiche Bildgrösse zu kommen.Die ersten drei Tabellen zeigen
die maximalen Belichtungszeiten mit Winkeln und Objektiv-Bildwinkeln für die Crop Faktoren 1.0, 1.3 und
1.6. Die nächsten drei Tabellen zeigen für dieselben Crop Faktoren die maximalen Belichtungszeiten
abhängig von der Deklination des Sternes.